一维信号的频域特征分析python

频域分析是按照频率观察信号特征。在一般情况下，我们分析信号习惯从时域方向开始，因为时域的分析更加直观，但频域的表示更加简洁，从这方面去分析对信号了解更加深刻。通过分析振动信号的频域特征准确地表征信号频谱信息，然后获悉在不同工况下部件运行时的健康状态。目前常用的频域特征参数包括重心频率、平均频率、均方根频率以及频率标准差。进行频域分析通常利用傅里叶变换开始。

首先来介绍一下计算频域特征的一个重要参量——功率谱，由于功率谱对功率信号还有其他随机信号的普遍适用性，故不采用简单频谱作为参考依据。但对于普通随机信号是可以直接采用频谱的。

功率谱定义：功率谱是原信号傅立叶变换的平方并除以采样点数N，称功率谱密度函数，被定义为单位频带内的信号功率，即表示了信号功率随着频率的变化情况。
而维纳-辛钦定理也指出：一个信号的功率谱密度就是该信号自相关函数的傅里叶变换。

功率谱单位为W/Hz。

import numpy as np
def get_fft_power_spectrum(y_values, N, f_s, f):
    f_values = np.linspace(0.0, f_s/f, N/f)
    fft_values_ = np.abs(fft(y_values))
    fft_values = 2.0/N * (fft_values_[0:N/2])    # 频率真实幅值分布，单边频谱图，再把所有点频率大小表示出来*2
    # power spectrum 直接周期法
    ps_values = fft_values**2 / N
    # 自相关傅里叶变换法
    cor_x = np.correlate(y_values, y_values, 'same')    # 自相关
    cor_X = fft(cor_x, N)
    ps_cor = np.abs(cor_X)
    ps_cor_values = 10*np.log10(ps_cor[0:N/2] / np.max(ps_cor))
    return f_values, fft_values, ps_values, ps_cor_values

上述式中返回值，f_values设置的范围，fft_values为所有信号点的傅里叶变换值，ps_values是直接周期法功率, ps_cor_values是自相关下的对数功率。

1. 重心频率：用来描述信号在频谱中分量较大的信号成分的频率，反映信号功率谱的分布情况。即对于给定的频带范围，低于重心频率的频率范围内包含的能量是信号总能量的一半。

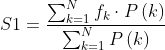其中P(k)为对应功率谱值，fk为对应点的频率幅值大小。低频幅值较大时，重心距离原点较近

x = np.loadtxt(./.txt)
N = len(x)
f_s = 12000
f_values, fft_values, ps_values, ps_cor_values = get_fft_power_spectrum(x, N, f_s, 2)
# 直接取周期法功率
P = ps_values
f = fft_values
S = []
for i in range(N//2):
    P1 = P[i]
    f1 = fft_values[i]
    s1 = P1*f1
    S.append(s1)
# 求取重心频率
S1 = np.sum(S)/np.sum(P)

2. 平均频率：功率谱值平均值。

S2 = np.sum(P)/N    #这个N是P的个数，并不是采样点数

3.频率标准差：重心频率为中心的惯性半径。我的理解是信号频率分布越离散，这个均方根频率越大。

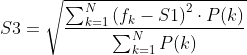  其中S1为重心频率。

S = []
for i in range(N//2):
    P1 = P[i]
    f1 = fft_values[i]
    s2 = P1*((f1-S1)**2)
    S.append(s2)
S3 = np.sqrt(np.sum(S) / np.sum(P))

4.  均方根频率：均方频率的算数平方根。均方根频率可以看做惯性半径，可以反馈出信号的频率分布。

公式：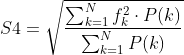

S = []
for i in range(N//2):
    P1 = P[i]
    f1 = fft_values[i]
    s2 = P1*(f1**2)
    S.append(s2)
S4 = np.sqrt(np.sum(S) / np.sum(P))

以上便是几种常用的频域特征及其python实现，希望多交流学习。